Bitácora Resolución de Problemas

 

Método Inductivo

Extraen conclusiones a partir de determinadas observaciones o experiencias particulares. Los argumentos inductivos parten de esta observación y luego generalizan. Obtienen una conclusión basándose en las probabilidades y en la intuición.

Se caracteriza por permitir llegar a una conclusión general a partir de observaciones repetidas de ejemplos específicos. 

Ejemplos: 

La valija de Catalina es negra.
La valija de Lucía es negra.
La valija de Pedro es negra.
Las valijas suelen ser negras.

 Método Deductivo

Extraen una conclusión a partir de las premisas. Si las premisas son verdaderas, la conclusión también lo es. Los argumentos deductivos poseen una base lógica, su conclusión está contenida en la información de las premisas.

Ejemplos: 

Los duraznos verdes no han madurado.
Este durazno está verde.
Este durazno no ha madurado.

 

 

Método Analógico

El método analógico es un proceso de razonamiento que se basa en la capacidad de asociación de la mente. Este proceso consiste en tomar una experiencia pasada y compararla con una experiencia actual, para llegar a conclusiones acerca de la experiencia actual apoyándose en otras experiencias ya ocurridas.

concluye pensamientos generales de casos generales o bien concluye pensamientos particulares de casos particulares. 

 

Pasos de Polya 

Problemas: En toda situación nueva que requiere la aplicación de alguna estrategia para su solución. si ello no se cumple, deja de ser un problema, en otras palabras si la situación a la que se enfrenta ya la ha resuelto en oportunidades anteriores o su solución es muy obvia, deja de ser un problema. 

1. Observar           
2. Planificar           
3. Experimentar
4. Decidir               
5. Compartir           
6. Argumentar

Según Polya, para resolver un problema se debe hacer una pausa, reflexionar, ejecutar pasos originales que no se habían ensayado antes de dar respuesta. 

Pasos fundamentales para la resolución de problemas, Según George Polya:

1.     Comprender el Problema: no se puede resolver un problema si no se entiende lo que se está pidiendo. El problema debe ser leído y analizado cuidadosamente. leerlo varias veces y preguntarse, ¿Qué debo encontrar?

2.     Formule un Plan: existen muchas formas de abordar un problema y determinar qué plan es más apropiado, entre ellos: a) Tabla o diagrama.  b) Buscar un patrón.   c) Ensayo y error

3.     Llevar a cabo un plan o aplicar la estrategia seleccionada: una vez decidido cómo enfocar el problema poner en práctica el plan. 

4.     Revisar y comprobar: ¿Satisface las condiciones del problema? ¿Ha resuelto todas las cuestiones implicadas en el problema? ¿Puede abordar el problema de manera diferente y aún así llegar a la misma respuesta? 

 

 Estrategia Ensayo y Error

Es una estrategia para la resolución de problemas. En esta se prueba una opción y se observa si funciona. si funciona, entonces se tiene una solución, si no, esto es un error, y se debe intentar otra opción.

 Ejemplo:

El dinero a disposición de un emprendedor es escaso. No lo malgastes. Invierte en lo que funciona.

 

  Estrategia Buscar un Patrón

Buscar un Patrón es una estrategia que puedes utilizar para buscar patrones en los datos con la finalidad de resolver problemas. La finalidad de dicha estrategia es buscar datos o números que se repiten, o bien buscar eventos que se repiten.

 

 Estrategia Diagrama o figura

Es otra estrategia para la resolución de problemas, que creo, les gustará a los que les gusta dibujar. En la figura se colocan todos los datos conocidos que da el problema y los datos que se pretende encontrar, esto nos ayuda a tener una mejor idea y visualización de lo que el problema pide.

 

 

Estrategia Resolver un Problema Equivalente

Esta estrategia se trata de poder resolver el problema comparando el problema con otro parecido, en el cual se conoce la solución del otro problema o la técnica para resolver y de esta manera se podrá llegar a resolver el problema.

 

Proporcionalidad o Porcentajes 

• Razón: Es el resultado de comprar dos cantidades y será siempre un número real.
• Proporción: Se le denomina proporción a la igualdad de dos razones.
• Porcentaje: Es una razón en la cual el consecuente es 100.

 Ejemplo: 

Se vendió un motor industrial obteniendo una ganancia de Q,3,450, lo que representó el 15% del costo. Cuánto costó el motor industrial y en cuánto de vendió?

 

                               3450            X  

                               15%          100%   = 23,000 (Monto Vendido)

 

                              23,000 - 3450 = 19,550 (Costo)

 

Lectura e Interpretación de gráficas

Las gráficas son representaciones abstractas de relaciones entre dos o más variables, también resumen y organizan la información, además de resaltar visualmente sus propiedades más importantes; las representaciones gráficas permiten establecer patrones y transmitir ideas de modo más sencillo.

La interpretación de tablas y gráficas estadísticas es útil para:

Comprender la información estadística que sobre diversos temas que proporcionan los medios de comunicación y poder evaluarla de forma crítica.

1. Entender la realidad social, económica y política.
2. Llevar a cabo investigaciones que requieran interpretar datos.
3. Discutir o comunicar las propias opiniones sobre la información que las estadísticas presentan.

 

Gráficas circulares

Denominadas también gráficas de pastel o gráficas del 100%, se utilizan para mostrar porcentajes y proporciones; estas gráficas nos permiten ver la distribución interna de los datos que representan un hecho, en forma de porcentajes sobre un total.

 

Gráficas de barras

Se emplean para ilustrar muestras agrupadas en intervalo. Está formada por rectángulos unidos a otros, donde la superficie de cada barra es proporcional a la frecuencia de los valores representados.

En el eje vertical se representan las frecuencias, y en el eje horizontal los valores de las variables. La altura de cada rectángulo es proporcional a la frecuencia del intervalo respectivo.

 

Gráficas de líneas

Muestran la relación entre dos variables cuantitativas. En este tipo de gráfico se representan los valores en dos ejes cartesianos. Las gráficas lineales se recomiendan para representar series en el tiempo y es donde se muestran valores máximos y mínimos; también se utiliza para varias muestras en un diagrama.

 

Proposiciones y valores de verdad

El ser humano, en su vida diaria, se comunica con sus semejantes a través de un lenguaje determinado (oral, escrito, etc.) por medio de las denominadas frases u oraciones. Estas pueden tener diferentes significados que pueden resumirse a las formas de verdaderas o falsas, siendo este el precedente fundamental para el desarrollo humano.

¿Qué es una proposición?

Es el significado de una idea, enunciado, conjunto de palabras o letras a las que se les puede asignar uno y solo uno de los valores de verdad, los cuales pueden ser verdadero (V) o falso (F) pero no ambos valores a la vez.

Por lo general, a las proposiciones se las representa por las letras del alfabeto desde la letra p, es decir, p, q, r, s, t… etc. Así por ejemplo podemos citar las siguientes proposiciones y su valor de verdad.

P: El campus Regional de Zacapa de la Universidad Rafael Landívar está ubico camino a Manzanotes, Zacapa.                                                                                   Valor de Verdad                              (V)

r: Quetzaltenango es un departamento de Guatemala.           Valor de Verdad                              (V)

s: Un quetzal es equivalente a 10 dólares.                             Valor de Verdad                              (F)

 

Expresiones no proposicionales

Son aquellos enunciados a los que no se les puede asignar un valor de verdad. Entre ellos tenemos a los exclamativos, interrogativos, imperativos y opiniones. Por ejemplo:

• ¿Cómo te llamas?
• ¡Salvemos el planeta!
• Borra la pantalla

 

ENUNCIADOS ABIERTOS

Una proposición abierta es un enunciado que da información que no se puede calificar como verdadera o falsa porque el sujeto no está especificado, por lo tanto no tiene valor de verdad. Por ejemplo:

X > 5

3 + z = 15

Ella juega pelota.

X  + 10 + 2 = 20

 

Clasificación de las proposiciones

Proposición simple:

Son aquellas proposiciones que se les puede representar por una sola variable, estas se llaman proposiciones simples o atómicas.  Es un enunciado que da solamente una información verdadera o falsa. Por ejemplo:

 P: El litro es una medida de capacidad

q: El metro es mayor que la yarda

 

 

Proposiciones Compuestas:

Cuando una proposición consta de dos o más enunciados simples, se le llama compuesta o molecular. Una proposición es compuesta cuando se construye uniendo dos o más proposiciones simples, y por ello, nos da más de una información. Por ejemplo:

Zacapa es departamento de Guatemala y pertenece a Centroamérica.

Otros ejemplos:

q  La capacidad de un recipiente se mide en litros o en metros cúbicos.

 

CONECTIVOS LÓGICOS

A partir de proposiciones simples es posible generar otras, simples o compuestas. Es decir que se puede operar con proposiciones, y para ello se utilizan ciertos símbolos llamados conectivos lógicos. Veamos una concreta definición de cada uno.

Negación

Dada una proposición p, se denomina la negación de p a otra proposición denotada por ~ p (se lee “no p”) que le asigna el valor de verdad opuesto al de p.

 

Conjunción

Dadas dos proposiciones p y q se denomina conjunción; de estas proposiciones  p ˄ q (a lo que se lee p y q) en donde cuya tabla de verdad es:

 

Disyunción

Dadas dos proposiciones p y q, la disyunción de las proposiciones p y q es la proposición p v q cuya tabla de valor de verdad es:

Condicional o Implicación

La proposición “p” se llama antecedente y la proposición “q” se llama consecuente de la condicional o implicación.

 

Recíproca

Si intercambiamos el antecedente “Guatemala es un país” y el consecuente “Guatemala pertenece a Centroamérica!, se obtiene una nueva proposición condicional.

 

Inversa

Si se niega ambos lados de la proposición directa, el antecedente y el consecuente, se obtiene la inversa de la proposición dada.

 

 Contrapositiva

Si el antecedente y el consecuente se intercambian y se niegan, se obtiene la contrapositiva de la proposición dada.

Ejemplo

“Si Guatemala no pertenece a Centroamérica, entonces Guatemala no es un país”.

 

Leyes del Álgebra Proposicional

Leyes de De Morgan

Las Leyes de De Morgan son muy útiles cuando se quiere encontrar equivalentes para proposiciones que se obtienen por negación de proposiciones compuestas.

“La negación de una conjunción equivale a la disyunción de las negociaciones”

~ (p ˄ q) Ξ ~ p v ~ q

“La negación de una disyunción equivale a la conjunción de las negaciones”

~ (p v q) Ξ ~ p ˄ ~ q

 

Negación de la bicondicional

Ejemplo:

Negar la proposición: “Un triángulo tiene 3 ángulos si y solo si un cuadrado tiene 4 lados”

P: Un triángulo tiene 3 ángulos.

q: Un cuadrado tiene 4 lados.

 

 

Teoría de Conjuntos

¿Qué es un Conjunto para mí?

Es una colección de objetos bien definidos por medio de alguna o algunas propiedades en común. Por objeto entenderemos no solo cosas físicas, como discos, computadores, etc. sino también abstractos, como son números, letras, etc.

Formas de Escribir un conjunto

Un conjunto se puede escribir en cualquiera de la siguientes formas:

Forma tabular, enumerativa o extensiva:

Escribimos dentro de llaves un listado de los elementos que lo forman, separándolos por medio de comas. Por ejemplo: A = { a, e, i, o, u}

Forma descriptiva o comprensiva:

Escribimos una variable para representar a los elementos del conjunto, luego, la proposición abierta que describe la propiedad común que los identifica. Ejemplo: A = {x/x es una vocal}

Forma gráfica:

Dibujamos una figura cerrada como un círculo, un cuadrado, triángulo u otro y colocamos adentro de ella los elementos del conjunto. Estas figuras se llaman diagramas de Venn.

 

Conjunto Universo o Referencial

Se llama conjunto universo o referencial a aquel que contiene a todos los elementos que estamos estudiando. Se nombra con la letra U.

El conjunto universo o referencial lo representamos gráficamente con la figura de un rectángulo. Adentro de este dibujamos las figuras que representan a los conjuntos que tienen a aquél como su referencia.

 

Operaciones con conjuntos

Consiste en reunir en un solo conjunto todos los elementos de dos o más conjuntos, el símbolo de operación unión es: U

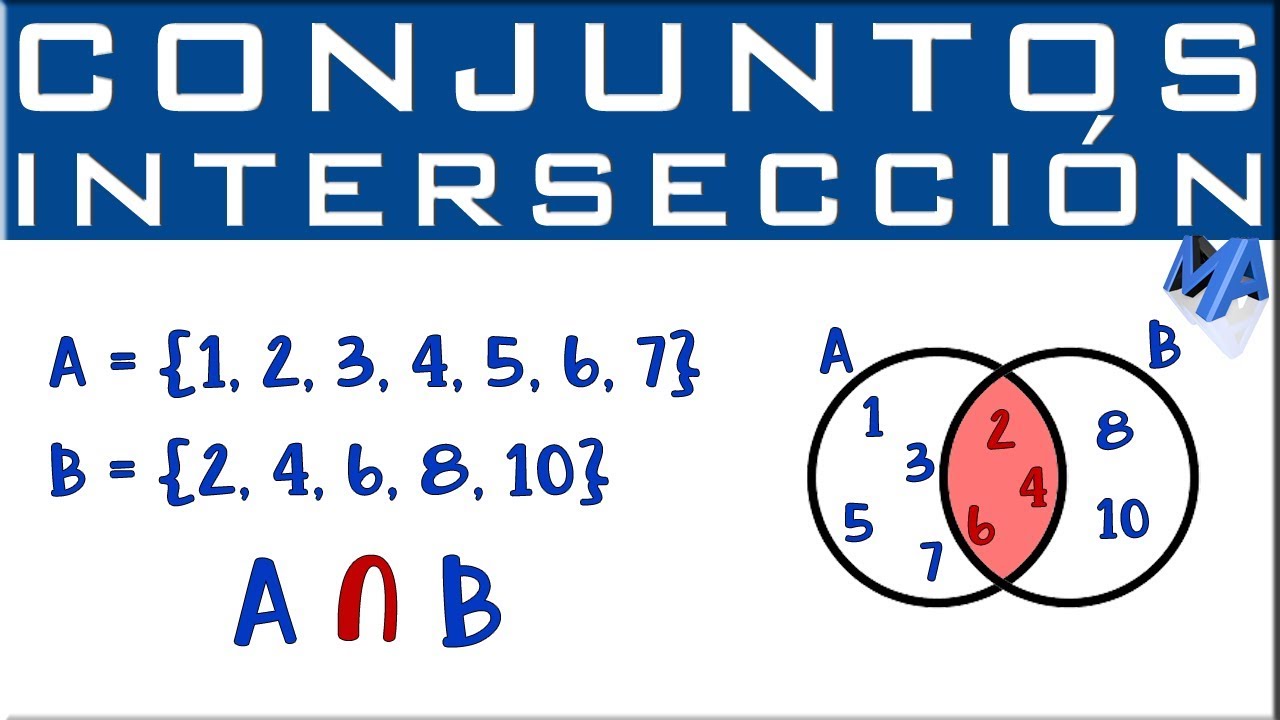
Intersección de conjuntos:

La operación intersección de dos conjuntos A y B se denota como A  Ո  B y se lee “A intersección B”.

Simbólicamente se expresa así: A Ո B = { x/x € A y x € B }

Es importante notar que aquí se necesita que el elemento x pertenezca al conjunto A y también pertenezca al conjunto B.

 

Diferencia de conjuntos

Dado dos conjuntos, esta operación consiste en formar un nuevo conjunto con los elementos diferentes del primero de ellos.

El símbolo de esta operación es: -

Dado los conjuntos A y B se llama diferencia de A menos B a un nuevo conjunto formado con los elementos que pertenecen a A y que no pertenecen a B.

A - B = { x/x € A y x € B }               

B - A = { x/x € A y x € B }

 

Complemento de Conjunto

Sea U el conjunto referencial o universal y A un conjunto particular contenido en este referencial, llamamos complemento de A al conjunto formado por los elementos que le faltan al conjunto A para ser igual al conjunto universo U.

El símbolo de la operación es:

Simbólicamente se expresa así: A     = { x/x € U y x € A }